如何计算非正态数据的过程能力指数

在精益六西格玛持续改进、统计质量管理和SPC中，评价过程的过程能力（Process Capability）都是必不可少的重要步骤。在用控制图确认过程处于统计受控状态之后，进行过程能力分析可以进一步判断过程能力是否达到客户的要求。过程能力分析也是六西格玛项目中评价过程基线和改进方向的重要手段。

对计量型的过程数据而言，如果数据服从正态分布，我们可以很方便地计算出相应的过程能力指数Cp、Cpk、Pp、Ppk等。但当数据呈现非正态分布状态时，如果直接按普通的计算过程能力的方法处理就会存在较大的风险。一般而言，对此类数据计算过程能力的方法主要有如下几类：

第一类方法是将非正态数据转换成正态数据进行计算，常用的转换方式包括我们在Minitab软件中经常用到的Box-Cox变换和Johnson变换等；第二类方法是拟合数据的实际分布，然后根据实际的分布估算其均值、标准差、分位数等，进而计算过程能力指数（比如在Minitab和JMP中，我们都可以比较方便地拟合连续分布）；第三类方法以非参数统计方法为基础，基于百分位数方法来计算过程能力。下面分别进行简单说明：

方法1：Box-Cox变换法的步骤

• 估计合适的Lambda（λ）值
• 计算出变换后的数据Y*
• 根据原数据的USL和LSL，计算求出变换后的USL*和LSL*
• 对Y*用USL*和LSL*计算过程能力指数
• 可计算短期过程能力和长期过程能力

方法2：Johnson变换法的步骤

• 根据Johnson判别原则确定转换方式
• 计算出变换后的数据Y*和最优变换公式
• 根据原数据的USL和LSL，计算出变换后的USL*和LSL*
• 对Y*用USL*和LSL*计算过程能力指数
• 此种方法通常只计算长期过程能力Pp和Ppk

Johnson变换的上述步骤是实际工作中中常用的步骤（逻辑）之一。而在某些行业（比如汽车行业）的相应规范中，在得出数据的最优变换后，通常需要根据最优变换，反向计算原始过程数据的相应分位数（0.00135、0.5、0.99865），用分位数法计算过程能力（参见方法3）。QuAInS系统能够很方便地帮助用户完成这两种逻辑的自动计算。

方法3：非参数计算法（分位数法）

使用这种方法时，我们不需对原始数据做任何转换，可以直接使用以下公式计算过程能力指数CP和CPK：

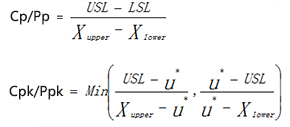
其中，X_upper和X_lower是随机数据X的百分位数，通常从数据总体（而非样本数据）中，取X_upper为X_99.865%，取X_lower为X_0.135%，对应于正态分布时覆盖99.73%的数据范围（±3σ）；也可取X_upper为X_99.5%，取X_lower为X_0.5%，以覆盖99%的数据范围。 u*表示过程的实际“位置(Location)”，根据ISO22514，u*通常取随机数据X的中位数（总体的中位数，而不是样本数据的中位数），有时也取X的算术平均数Xbar（总体的均值）。在各行业的实际使用中，此方法有时用来计算短期过程能力，有时用来计算长期过程能力。

方法3看起来比较简单，但因为其中的分位数需要使用总体而不是样本数据的分位数，因此往往需要从样本数据中出发，确定总体的分布，这样才能准确地进行计算。

过程能力分析是统计过程控制SPC、设备及过程能力评估、工业统计及六西格玛持续改进DMAIC中十分重要的内容，也是我们评价过程基线及改进方向和目标的重要工具。因此，在六西格玛项目中，过程能力分析是测量阶段的一项重要工作，其中，检验数据的正态性以及采用相应的方法计算过程能力就显得尤为重要了。

本文参考文献包括但不限于：

1. QuAInS系统开发手册

2.《六西格玛管理》及《六西格玛管理统计指南》，中国人民大学出版社

3. ISO 22514相关内容

4. “Statistical Procedures for Machine and Process Qualification” of Q-DAS

5. Minitab及JMP软件相关技术文献