箱线图(Box Plot)的几个关键技术细节

对经常做质量数据分析的人而言，箱线图(Box Plot)可以说是再常见不过的了。从应用而非理论的角度出发，虽然我们不一定需要了解其背后的每一个技术细节，我们在本文中讨论的几个关键点无疑是需要我们注意的。

箱线图的构成及相关计算

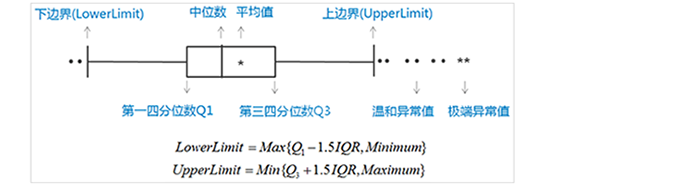
上图中，IQR为四分位距，IQR=Q3-Q1；由此可见，箱线图上下两端的引线长度可能是不相同的。

箱线图常见应用

1. 观察数据的总体状态

这也是箱线图最常用的作用，从中我们可以观察到数据的分位数、中位数及平均值等统计信息，并可以根据中位数和平均值的相对位置大致判断数据的分布形态。

2.识别数据中的异常值

在箱线图中，上图中的下边界和上边界也成为内限，此外箱线图还有外限（Q1－3IQR和Q3+3IQR），箱线图上，超过内限的数据都被认为是异常值，其中在内限和外限之间的数据被称作温和异常值（mild outliers），在外限之外的数据被称为极端异常值(extreme outliers)。

用箱线图识别异常值的好处：
一批数据中的异常值是值得关注的，我们通过分析异常值产生的原因，往往能够发现解决问题的机会。虽然箱线图判断异常值的方法看起来有一定的任意性，但经验表明其在实际工作中具有较大的实用价值，其在处理需要特别注意的数据方面表现不错。

事实上，箱线图识别异常值的方法与其他经典方法有所不同，这使其具备一定的优越性：一方面，基于3倍西格玛法则或z分数方法都是以假定数据服从正态分布为前提的，但实际数据往往并不严格服从正态分布。而且，它们判断异常值时都需要计算数据的均值和标准差，并以此作为判断异常值的标准，而均值和标准差的稳定性很小，而且异常值本身会对它们产生较大影响（这样产生的异常值个数不会多于总数0.7%）。因此，如果用这两种方法来识别非正态分布数据中的异常值，其作用是比较有限的。而箱形图基于实际数据，不需要事先假定数据服从特定的分布，而只是真实地表现数据的本来状态；另一方面，箱形图基于四分位数和四分位距来判断异常值，而四分位数具有一定的稳定性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，可见，箱形图识别异常值的结果相对比较客观。

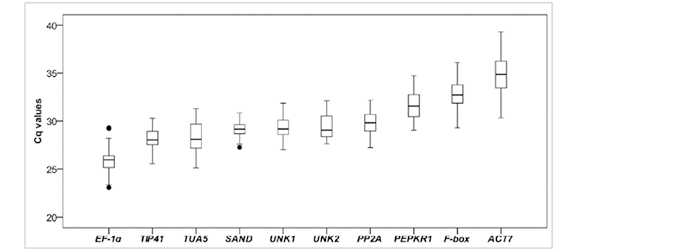
3. 比较几组数据的形状

如下图所示，我们将按照一定规则分组的几组数据放在同一张图上用箱线图进行展现，就可以比较各组数据的情况，比如总体而言，哪组数据相对较高（或较低），哪组数据相对比较集中，每组数据在所有数据中处于什么位置等等，这些都能为我们进一步分析数据提供重要的信息。