SPC控制图的选择[完整版]——单因素，多因素质量控制

统计过程控制（SPC: Statistical Process Control）是实际质量管理实践中用来进行在线或离线、实时或非实时过程监控、能力分析的常用方法。常用的控制图根据其分析对象的多少可以分为单因素控制图(Univariate Control Chart)和多因素控制图(Multivariate Control Chart)。

在统计过程控制（SPC）中，单因素控制图(Univariate Control Chart)用来检验过程单个质量参数是否受控的情况，常用的单因素控制图包括：

• 休哈特控制图之Xbar-R/S控制图
• 休哈特控制图之I-MR控制图
• 休哈特控制图之C控制图（用于固定样本量的缺陷数）
• 休哈特控制图之U控制图（用于可变样本量的单位缺陷数）
• 休哈特控制图之P控制图(用于可变样本量的不合格品率)
• 休哈特控制图之NP控制图（用于固定样本量的不合格品数）
• CUSUM控制图（累积和控制图）
• EWMA控制图（指数加权移动平均控制图）

其中，休哈特控制图中，前两种主要用于监控连续型测量数据，而后四种主要用来监控属性测量（离散型）数据。 在使用这些控制图时，我们通常只针对一个过程输出变量。通常而言，对于上述控制图的选择，我们可以遵循如下大致的路径：

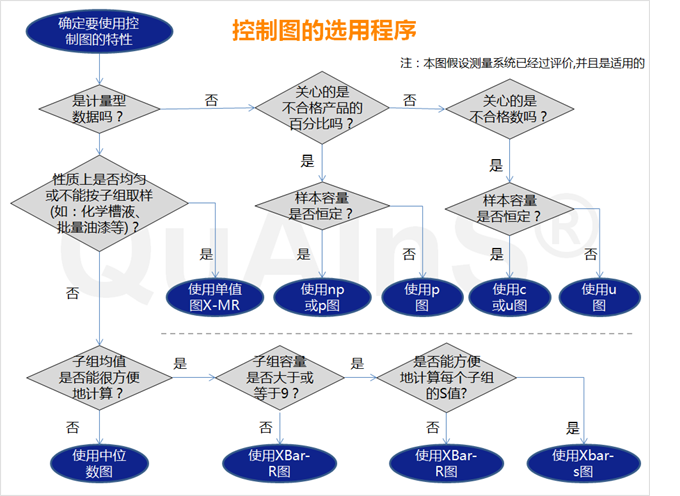
上述选择路径图在很多国内的质量管理书籍中都能见到。

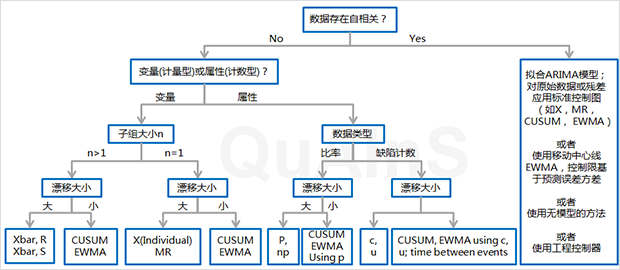
不过事实上，我们在使用这些控制图方法时，通常假定过程数据是不存在自相关性的。如果考虑过程数据的自相关性，单因素控制图的完整选择路径应如下：

多种单因素过程控制方法适用的情形

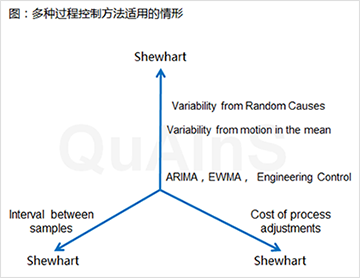
从上图左轴可以看出，随着样本抽样间隔的增加，休哈特控制图将越来越变得适用，因为样本较大的抽样间隔通常会使自相关效应失效；而随着样本抽样间隔的减小，自相关效应将变得更加重要，此时我们很可能需要使用ARIMA或EWMA方法。而从右轴可以看出，过程调整的成本增加会促使我们使用休哈特控制图来监测过程；而在另一方面，如果过程调整成本较低，将使得我们可以使用一些工程过程控制系统。在纵轴上，当随机因素或噪声在均值的移动中处于主导地位时，休哈特控制图会变得更加适合；而如果均值的移动更多地与随机噪声有关，我们又会使用ARIMA或EWMA类型的方法，或者工程控制器。

那么，当需要监控的变量不止一个且相关呢？

一种方法是对每个变量分别使用单因素控制图，但这种方式有时候是有效的，但也有时候会无效甚至出现有误导性的结论，这时候，我们就需要使用多因素控制方法了，它们能将不同参数结合起来考虑。

在多因素控制图中，“Hotelling T² ”控制图与Xbar控制图类似，另外EWMA控制图也有适用于多因素质量监控的版本。多因素控制图在变量个数不太多（比如10个以内）的时候效果比较明显，而当变量个数增多时，传统的多因素控制图却不是很有效，这时候我们通常需要对变量个数进行降维处理，进行降维的有效方法之一是使用主成分分析法。

比如在很多时候，一种轴承的外径和内径就是两个彼此相关的变量。这时，我们或许可以用单因素控制图对轴承的外径和内径分别进行监控，但这有时却具有一定的误导性。在如下的图形中，X1和X2在被用单因素控制图单独进行监控时并没有发现异常，这时X1和X2都应在其控制限内，等同于点（X1,X2）落在如下图中的阴影区域，但是看起来有一个点与其他点似乎有所不同。这时，如果我们需要提升质量监控的效率，就需要考虑多因素控制图了，其必要性从下面两幅图中可见一斑。

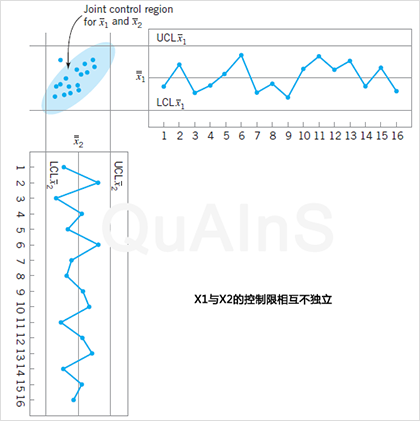
由于在当今的生产实践中，自动测量同一产品的多个变量变得相对容易，比如在一些化工厂和半导体公司，保留产品的数百个变量的测量数据是一种很常见的情况。在这种背景下，多因素控制图也开始被越来越多地重视。