重要的指数：Cp，Cpk，Cpm，Cpmk，Pp，Ppk，Cmk,，Cgk

过程能力分析和过程绩效分析师评价过程满足预期要求的能力及其表现的方法，也是精益六西格玛项目中评价过程基线及改进方向和目标的重要工具。其假设前提是过程输出服从正态分布。

过程的波动

• 过程固有波动：是仅由普通因素影响而产生的过程波动，它可以通过控制图的RBar/d₂来估计。
• 过程的总波动：是由普通因素和特殊因素影响而产生的波动，它可由样本标准差s估计。
• 过程能力PC：过程固有波动的6σ范围。
• 过程绩效PP：过程总波动的6σ范围。

注：如下指数计算时，涉及短期(Within)标准差和长期(Overall)标准差。在计算短期标准差时，若子组大小不等，QuAInS使用合并标准差法进行计算。

过程能力指数Cp与Cpk

潜在过程能力指数Cp：通常，我们将6σ范围视为过程的自然波动范围。为了把过程的自然输出能力与要求的容差(T=USL-LSL)进行比较，著名质量专家朱兰引入了“能力比”的概念，即第一代的过程能力Cp。当过程处于统计受控状态时，定义Cp=容差/自然波动范围=(USL-LSL)/(6σ)，M=(USL+LSL)/2称为规范中心。

在过去和通常情况下，我们通常称Cp≤1时，过程能力不足；1≤Cp≤1.33时，过程能力尚可；1.33≤Cp≤1.67时，过程能力充足。但在经济繁荣，产品数量急剧增长、高科技蓬勃发展的今天，我们常常提出更高的要求。比如在六西格玛管理中，一个标志性的要求是Cp≥2，即要求(USL-LSL)≥(12σ)。

但是，Cp是假定过程实际输出的均值与规范中心M是重合时的过程能力，其反应的是过程的潜在能力（而不是实际能力），所以在一般场合下，Cp称为潜在过程能力指数。

实际过程能力指数Cpk：在大多数情况下，过程实际输出的均值μ与规范中心M是不重合的。Cpk的引入正是为了在进行过程能力分析时将μ的影响考虑进来。Cpk称为实际过程能力指数。

Cpk={min[(USL-μ), (μ-LSL)]}/(3σ)=min(Cpu, Cpl)，其中Cpu为单侧上限过程能力指数，在仅有上规范限的场合即可使用；Cpl为单侧下限过程能力指数，在仅有下规范限的场合即可使用。

Cp和Cpk的应用：当μ=M时，Cp=Cpk；当μ≠M时，Cpk<Cp；如果过程的双侧规范限都给定，此时Cp有意义，我们就能够同时考虑Cp和Cpk以便对整个过程的状况有比较全面的了解。例如：

• 当Cp和Cpk都较小且差别不大时（比如Cp=0.79，Cpk=0.71），说明过程的主要问题是波动(σ)太大，进行过程改进时应首先降低过程的波动。
• 如果Cp较大，而Cpk很小（如Cp=1.32，Cpk=0.65），二者差别很大，则说明过程的主要问题是过程的实际均值μ偏离规范中心M太多，因此进行过程改进时应首先移动μ，使其更接近M。
• 如果Cp本来就比较小，而Cpk更小（比如Cp=0.84，Cpk=0.35），二者差别较大时，说明过程的实际均值μ和波动σ都有问题，进行过程改进时同擦很难过先移动μ值，使之更接近M，然后设法降低过程的波动。

过程能力指数Cpm和Cpmk

为了强调质量特性偏离目标值造成的质量损失，将目标值m(Target)引入计算，就得到Cpm和Cpmk：

Cpm=(USL-LSL)/(6σ₁)，其中σ₁²=σ²+(μ-m)²。Cpmk²=Cpk²/[1+(μ-m)²/σ²]。

也可以这样计算Cpm：Cpm=min(USL-m, m-LSL)/3*sqrt(s²+(μ-m)²)，其中s为样本标准差

第二代过程能力指数Cpm：质量特性偏离目标值m而导致的损失通常被认为近似于对称的平方误差损失函数，即质量损失函数。Cpm指数反应了过程实际输出μ和目标值m之间的偏差，主要用于反应过程的期望损失，这体现了田口的质量损失函数的理念。而且在目标值m与规范中心M不重合时，Cpm比Cpk能更好地描述过程输出μ和目标值m（而不是规范中心M）之间的偏差。Cpm有时也被称为第二代过程能力指数。

混合能力指数Cpmk：Cpmk在Cpk和Cpm的基础上，能够更加灵敏地反应过程实际输出的均值μ与目标值m之间的偏差。

过程绩效指数Pp与Ppk

过程绩效指数从过程总波动的角度考察过程能力，有时也被称为长期过程能力指数。在考虑过程绩效时，不要求过程稳定，也不要求过程输出的质量特性一定服从正态分布，因为过程在较长时期内产生的数据很难保证具有正态性。它们的计算公式为：

• 潜在过程绩效指数Pp：Pp=(USL-LSL)/(6s)；其中s为样本标准差；
• 单侧上限过程绩效指数Ppu：Ppu=(USL-XBar)/3s；
• 单侧下线过程绩效指数Ppl：Ppl=(XBar-LSL)/3s；
• 实际过程绩效指数Ppk：Ppk=min(Ppm，Ppl)。

长期过程能力与短期过程能力

在管理实践（特别是六西格玛管理实践）中，我们通常还使用六西格玛水平Z来评价过程能力。

短期过程能力是指过程仅受随机因素影响时其输出特性波动的大小，是过程的固有能力；长期过程能力是过程在较长的时间里表现出来的过程输出特性波动的大小，此时过程不仅受随机因素影响，而且还受到其他非随机因素的影响。

时间经验表明，过程的长期能力和短期能力的西格玛水平之间平均约有1.5σ的飘移，即Zlt=Zst-1.5。

机械设备能力指数Cm与Cmk

机械设备能力指数用来评估一台机械设备的稳定性，通常能在进行设备验收时使用，是短期的机械设备能力指数；它强调设备本身因素的影响，针对的是机械设备本身，而不是其产出的零件。

实施Cm、Cmk评估时，在人员、原材料、加工方法、测量系统、生产模具等都不能发生改变的前提下，进行连续抽样：用同一测量仪器在确定的测量位置上、在相同的条件下测量至少25个连续生产的样件（一般取50个样件）。

Cm、Cmk的计算公式与Cp、Cpk的计算公式相同。不同之处在于取样：Cm、Cmk的样品是连续取的，而Cp、Cpk的取样通常有一定的时间间隔（Interval）。

量具能力指数Cg与Cgk

量具能力指数用来评估一台量具的测量能力是否和被测产品的公差要求相匹配。

进行Cgk分析的方法： 1. 用比待评估的量具更高一级精度的量具（“参考量具”）来确定测试样品的真实测量值（“基准值”），如果没有合适的“参考量具”或对测量结果有怀疑，则只能测定Cg值；2. 让一个操作员用待评估的量具在该测试样品上的同一位置连续测量至少25 次（一般为50次）； 3. 用获得的数据计算出平均值或平均偏移值、标准差s； 4. 计算被测产品的公差T=USL-LSL； 5. Cgk通常要在测量系统GRR分析前评估好。

计算公式：

Cg=0.2T/6s

Cgk=min {[(基准值+0.1T)-测量均值]/3s, [测量均值-(基准值-0.1T)]/3s}; 或Cgk=(0.1T-|平均偏移值|)/2s。各个公司的Cgk的计算公式可能会略有不同，比如其中的“0.1”通常在0.1~0.2之间变化。

各指数的区别

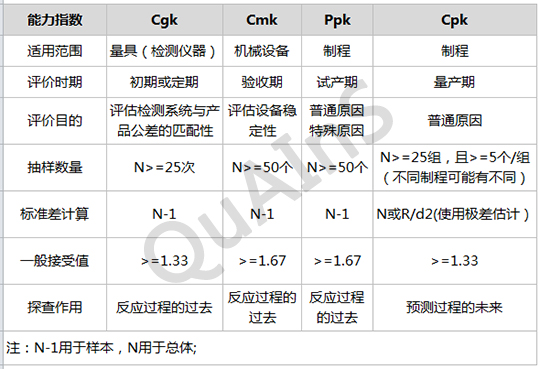
参考文献：《六西格玛管理》(第二版)，中国质量协会组织编写，马林、何桢主编，中国质量协会六西格玛黑带注册考试指定辅导教材